 | ２学年 「第３章 図形と方程式 第２節 円」 授業者 鹿本高等学校 相葉 忠臣 教諭 |
 授業映像 | インタビュー |  学習指導案 |
◆ ＩＣＴ活用のポイント
| （１） | 教師の活用 | |
・ | 前時の振り返りをする際に、教科書の内容を分かりやすく提示するために活用する。 | |
| ・ | 課題内容の理解を深めるために用いる教科書の図を分かりやすく提示するために活用する。 | |
・ | 課題の内容を別の視点でとらえるために、教科書の図を分かりやすく提示する。 | |
・ | 授業内容をまとめる際に、教科書の内容を提示し、分かりやすく振り返るために活用する。 |
◆ 本時の展開
| （１） | 目標 | ○ | 円と直線の位置関係について、２次方程式の判別式を活用して調べることができる。 |
○ | 円と直線の位置関係について、円の中心から直線までの距離と円の半径の大小関係を活用して調べることができる。 | ||
| （２） | 展開 |
| 過程 | 学習活動と主な発問(T) | 指導上の留意点・評価 | 備考 ICT活用 |
| 導入５分 | 前時の振り返り、 ①円と直線の共有点座標を求める。 ②判別式Dと、円と直線の位置関係を整理する。 【一斉】 | ・円と直線の連立方程式を解く中で、xについての２次方程式に着目し、実数解の個数と判別式D＝b2-4acの符号と、円と直線の位置関係を、教科書の表を用いて再確認する。 | 教科書の図の提示 【書画カメラ】
|
| 展開40分 | 【応用例題３】 円x2+y2=1と直線y=x+kが異なる２点で交わるとき、定数kの値の範囲を求めよ。 【一斉】 （T）ｙにx+kを代入して整理するとどんな式になりますか？ （T）２次方程式の判別式は？ （T）異なる二点で交わるときのDの条件は何ですか？ （T）２次不等式の解はどうなりますか？
【個別】 （T）生徒を指名して解答を板書させる。 板書された解答の確認をする。 【一斉】 円の中心から直線までの距離と円の半径を比較して、円と直線の位置関係を確認する。 【グループ】 （T）円と直線の位置関係について、図に描いている意味を隣同士で話し合いなさい。（C）円の中心から直線までの距離dと円の半径rを比較して、d<rならば異なる２点で交わる。 【一斉】 （T）点と直線の距離の公式は覚えていますか？ 応用例題３について、円の中心から直線までの距離と円の半径を比較することによる別解を考察する。 応用例題３の円と直線について、「(2)共有点を持たないとき、定数kの値の範囲を求めよ。」の別解を作る。 【個別】 解答の確認
| ・連立方程式を解く中で、yにx+kを代入することでyを消去してxの２次方程式を作る。
【知識・理解】 【表現・処理】 ・机間指導を行い生徒の理解度を確認する。 【意欲・態度】 ・接するD=0、共有点を持たないD<0を理解し、活用できる。 【知識・理解】 【技能】
【知識・理解】 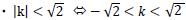 が理解できる。【技能】 ・生徒を指名して解答を板書させる。 | 教科書の図の提示
教科書の提示
|
| 終末５分 | 本時のまとめ 家庭学習課題の提示 次回の予告 【一斉】 | 教科書の内容を提示 【書画カメラ】 |
を確認する。
を活用できる。
