２学年　「２つの曲線の間の面積」
授業者　熊本農業高等学校　櫻井　祐二　教諭




授業映像
学習指導案		 


◆　ＩＣＴ活用のポイント

 （１）

教師の活用

　・
　

例題４の解説時に、投影しているグラフの上から直接マーカーで書き込みを行い重要な部分を強調する。

　・

ワイヤレスキーボードを利用し、教室内を自由に動くことができる。


 （２）

生徒の活用

　・
　

Grapesを利用することでグラフを作図できなくてもＰＣ上で確認でき、積分の式を立てることができる。


◆　本時の展開

　（１）目標

２つの関数のグラフの間の面積が、定積分によって求められるようにする。

　（２）展開 



過程

学習活動と主な発問(T)
　予想される児童の反応(C)

指導上の留意点・評価

備考
ICT活用
導入15分

１ ２つの関数のグラフと直線 x=a、x=bで囲まれた図形の面積の公式を確認する。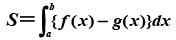

　　
・求める手順を確認する。
①交点の座標を求める。
②グラフの上下関係を確認。 ③求める面積Sを定積分で計 算する。

課題２つの関数のグラフと直線 x=a 、x=bで囲まれた図形の面積の公式利用の定着。		○前回の学習内容（面積の公式）を振り返る。


○グラフを想像できない生徒もいるため、丁寧に説明する。





Grapesを用いてグラフを表示。

展開30分

２ 問13を考えさせる。


(1)放物線 y=x2-9 、直線 y=2x-1 (2)放物線y=x2+5x、直線y=x+3

・グラフを描き、位置関係・交点を確認する。
・公式を利用して、面積を計算する。
・問13を板書する。
・問13で利用した関数をGrapesに入力する。

○手順①②③のとおり考えさせる。

・評価【技能】（PCノートでグラフを表示しているか）
・評価【技能】（ノートに面積を求める式を立て計算していか）
○積分範囲は、交点の座標を見ることで確認できる。

○問13が解けたら、隣の生徒と結果を確認してみる。

生徒は、グラフの位置確認にGrapesを利用する。

グラフを拡大縮小して交点を確認する。

終末５分３ 本時のまとめ。
・囲まれる図形の面積を求める
公式を確認する。

○面積を求める手順①②③の確認をする。